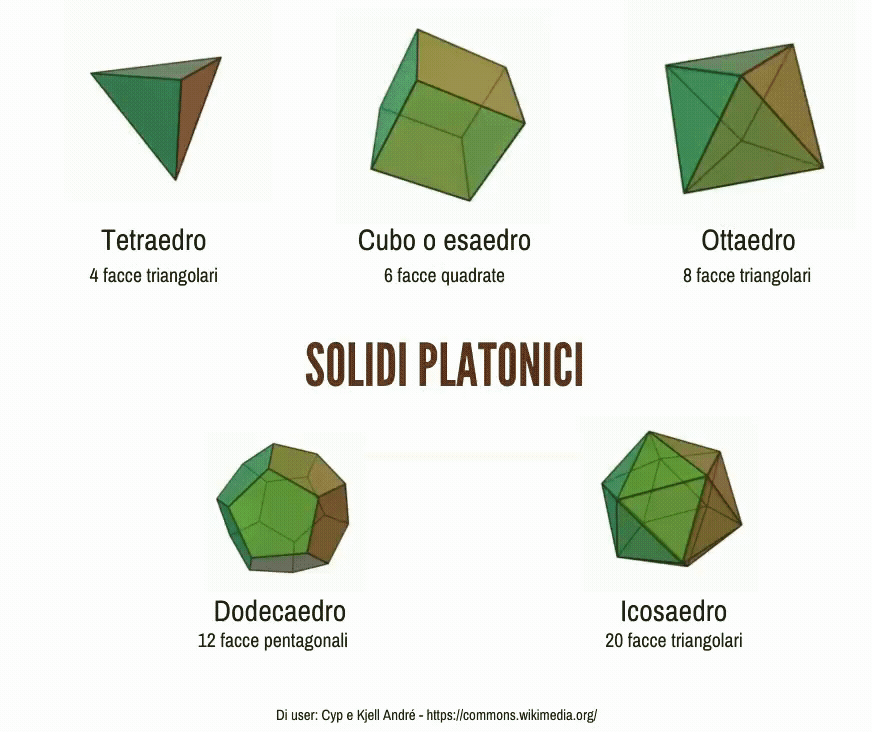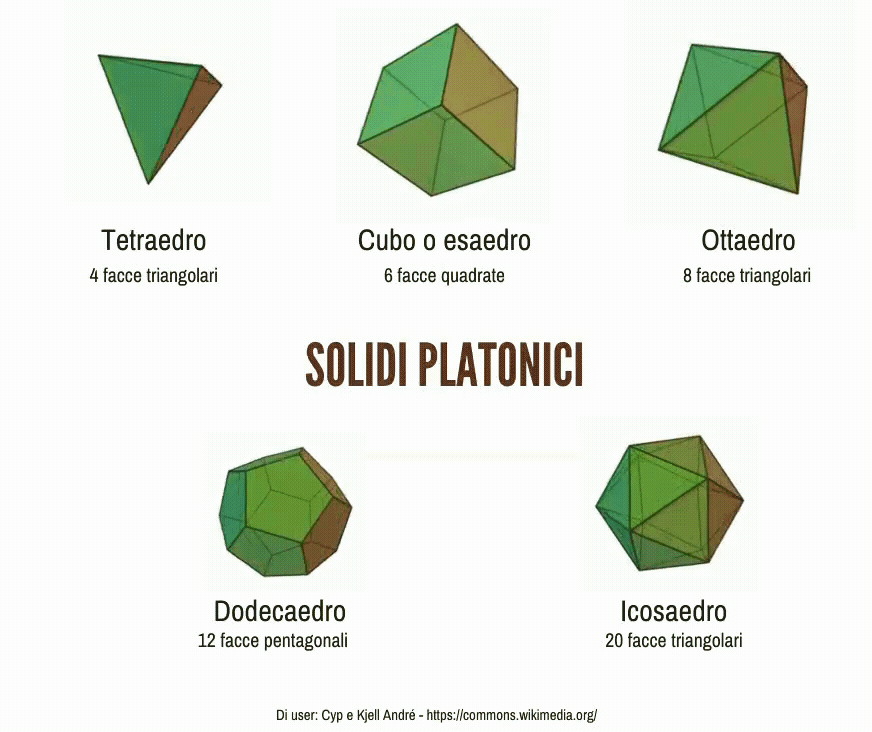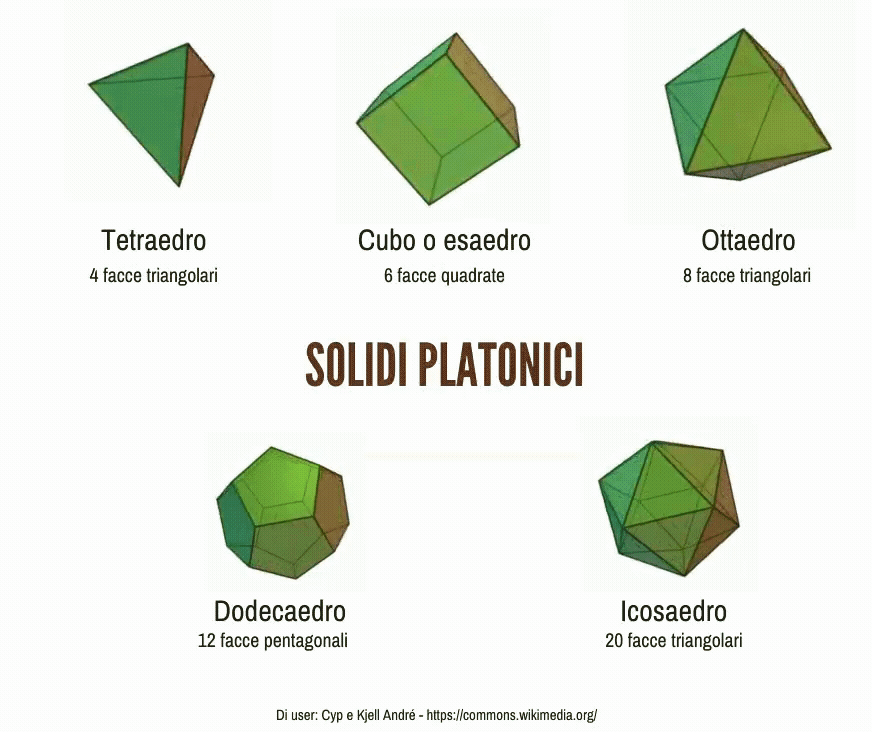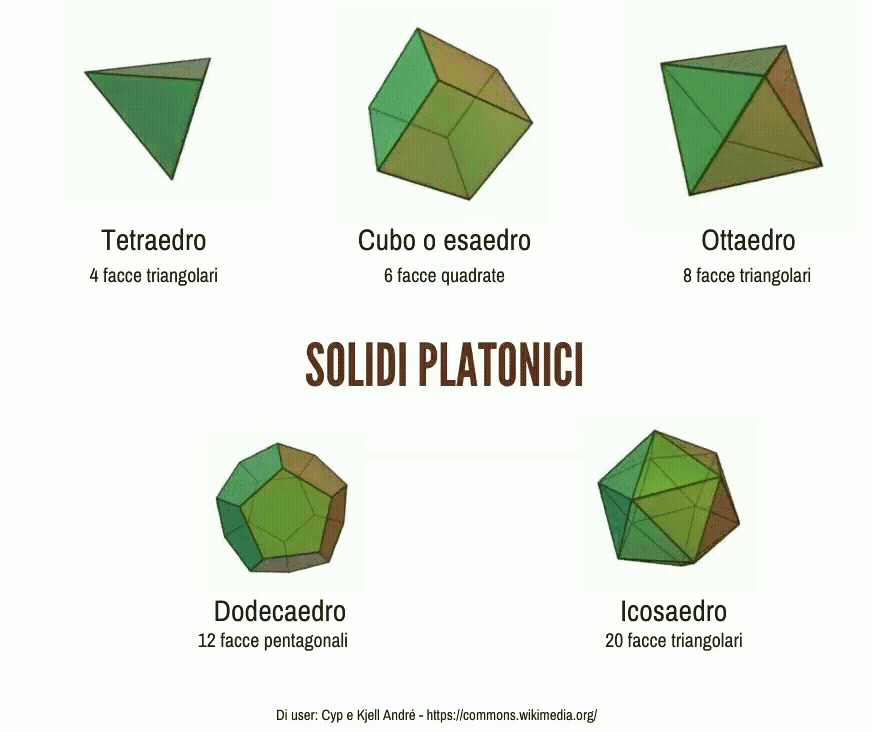
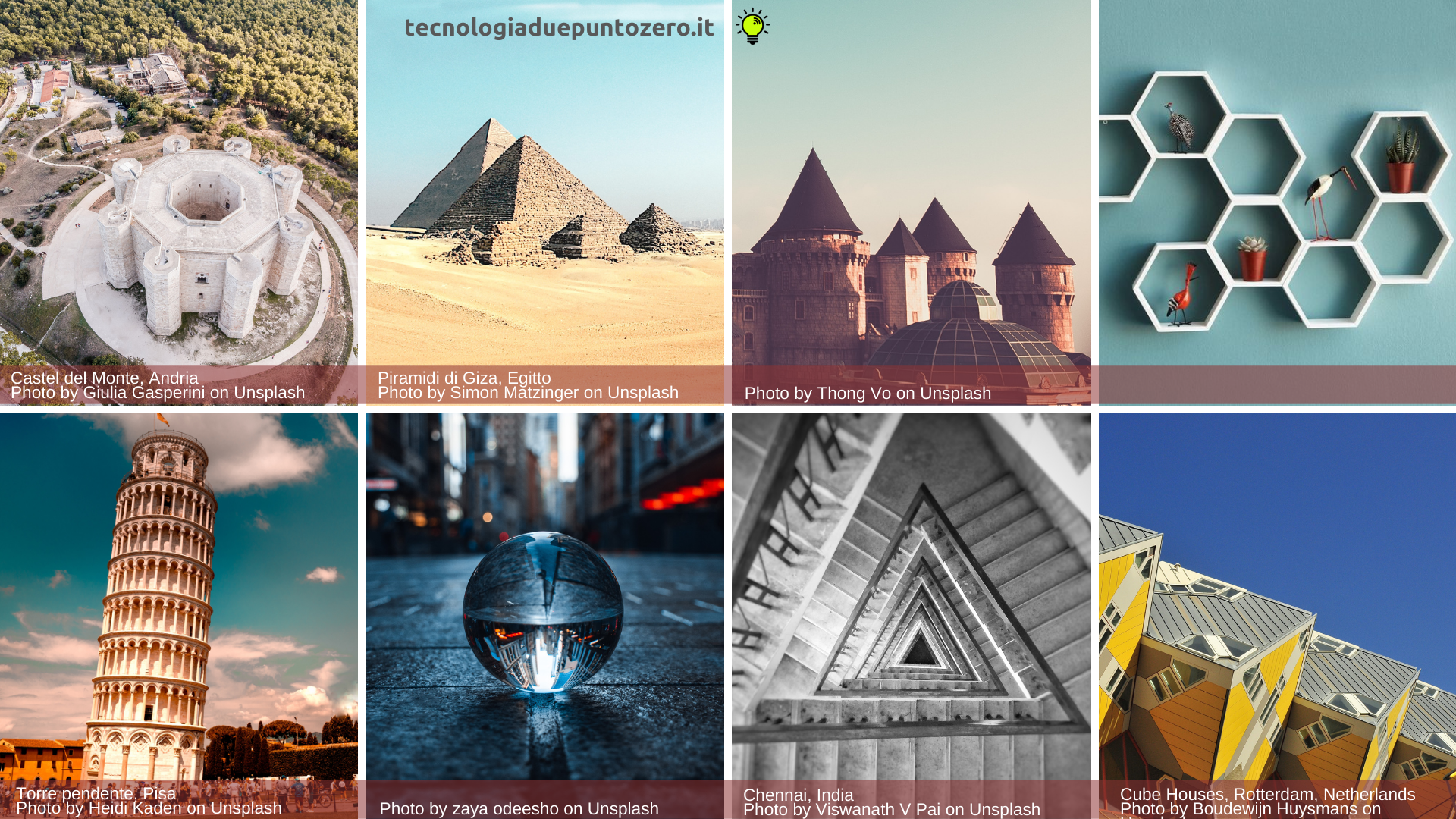
Che differenza c’è tra un solido e una figura piana? Quali figure solide conosci? Quali solidi ti vengono in mente guardando queste immagini?
Proviamo a fare un esercizio…
I solidi geometrici
I solidi sono figure geometriche o corpi aventi tre dimensioni.
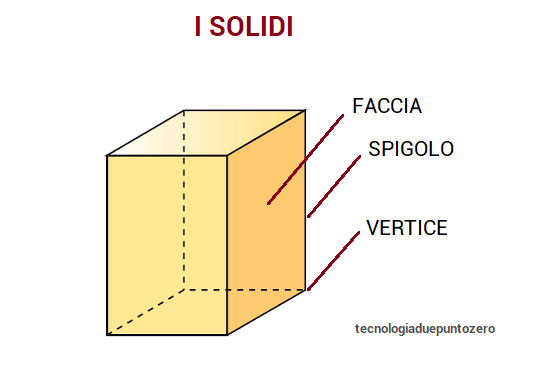
Vediamo un po’ di nomenclatura:
- le facce; sono i poligoni che compongono il solido
- gli spigoli; sono i lati delle facce
- i vertici; sono le estremità degli spigoli
Il volume è tutto lo spazio contenuto all’interno della figura solida.
I solidi si possono suddividere in:
- poliedri, delimitati da un numero finito di facce piane poligonali. Alcuni esempi sono i solidi platonici, i prismi e le piramidi.
- solidi di rotazione, ottenuti dalla rotazione di figure piane attorno ad un asse; hanno almeno una superficie curva. Alcuni esempi sono il cilindro, il cono e la sfera.
Se può esserti utile, scarica lo schema in formato pdf
SOLIDI schema mappaI
I poliedri
Sono solidi formati da facce piane poligonali. Appartengono ai poliedri ad esempio
- i solidi platonici
- i prismi
- le piramidi.
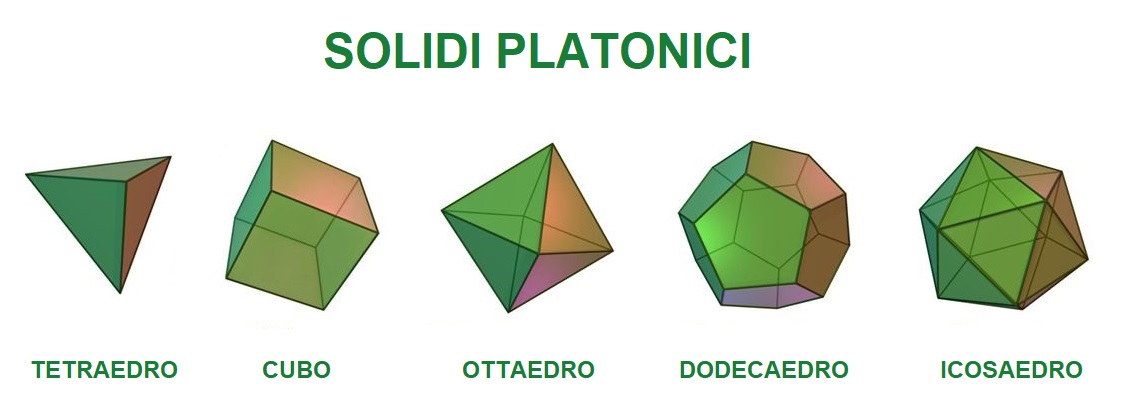
I solidi platonici (o poliedri regolari)
Un poliedro si dice regolare se tutte le sue facce sono poligoni regolari congruenti fra loro. I poliedri regolari sono cinque, e sono detti anche solidi platonici.
I prismi
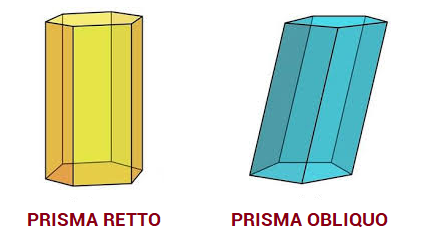
I prismi hanno due basi poligonali congruenti e parallele tra loro.
Si possono avere:
- prismi retti: le cui facce laterali sono rettangoli
- prismi obliqui le cui facce laterali sono parallelogrammi
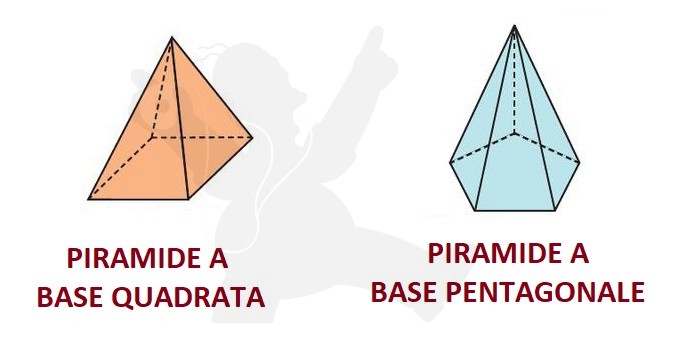
Le piramidi
Le piramidi hanno una sola base poligonale e un vertice opposto alla base.
Le facce laterali sono triangoli aventi in comune il vertice della piramide.
Si dice altezza di una piramide il segmento che dal vertice cade ortogonalmente sul piano contenente la base.
Si possono avere:
- piramidi rette
- piramidi oblique
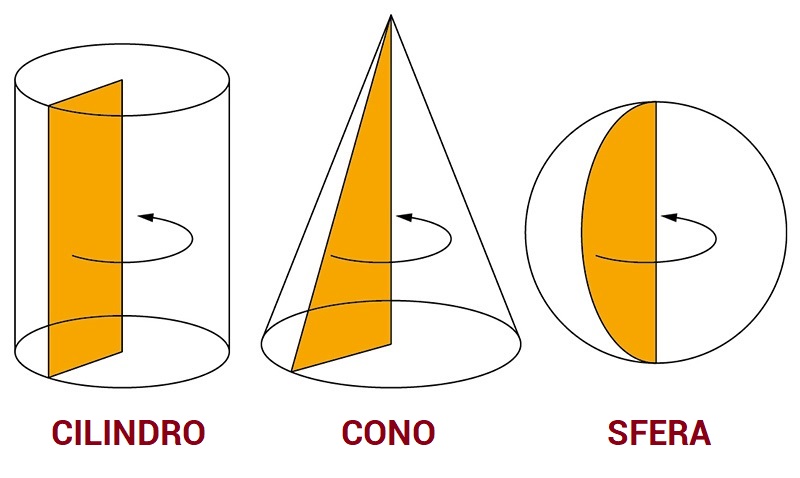
I solidi di rotazione
Si ottengono dalla rotazione di una figura piana attorno ad un asse. Pertanto, hanno almeno una superficie curva.
Si dice asse di rotazione la retta attorno a cui ruota la figura piana per formare il solido.
Sono solidi di rotazione:
- il cilindro, che si ottiene dalla rotazione di un rettangolo intorno a un lato
- il cono, che si ottiene dalla rotazione di un triangolo rettangolo intorno ad un cateto
- la sfera, che si ottiene dalla rotazione di un semicerchio intorno al proprio diametro
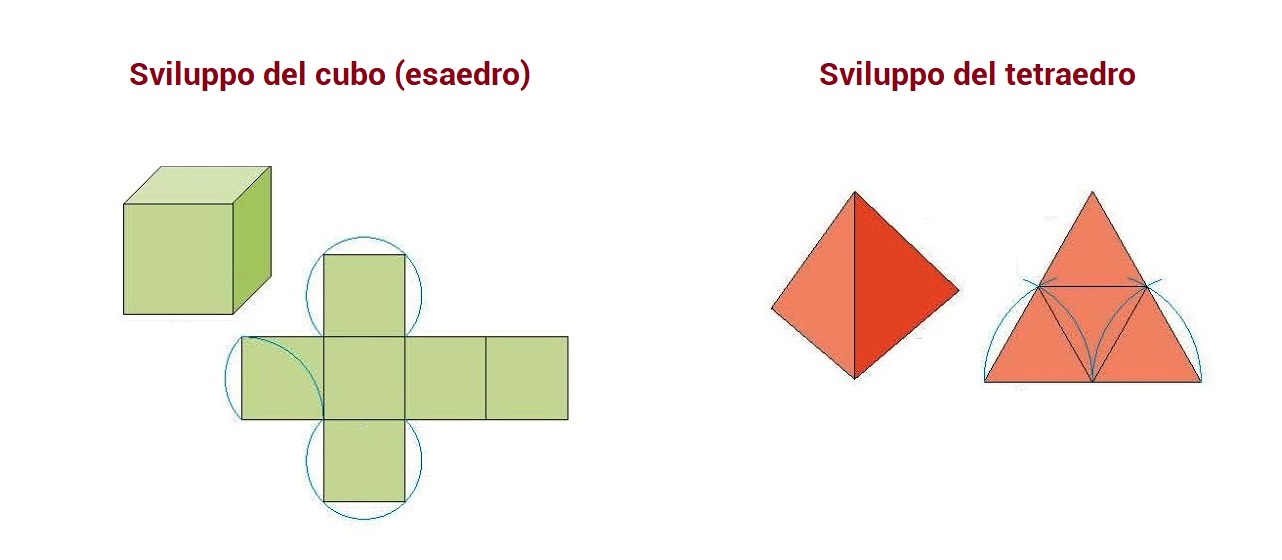
Lo sviluppo di un solido
Lo sviluppo di un solido è la figura piana che si ottiene riportando su un piano tutte le facce che lo compongono.
Consiste in certo numero di figure piane accoppiate lungo alcuni lati, che possono essere piegate in modo da chiudersi e formare il solido. Lo sviluppo piano è uno strumento concreto utile per costruire poliedri di carta.
Lo stesso solido può essere costruito a partire da sviluppi piani differenti: l’insieme dei poligoni presenti è sempre lo stesso (sono le facce del solido), ma la figura piana che queste formano può essere differente.
Alcuni esempi:
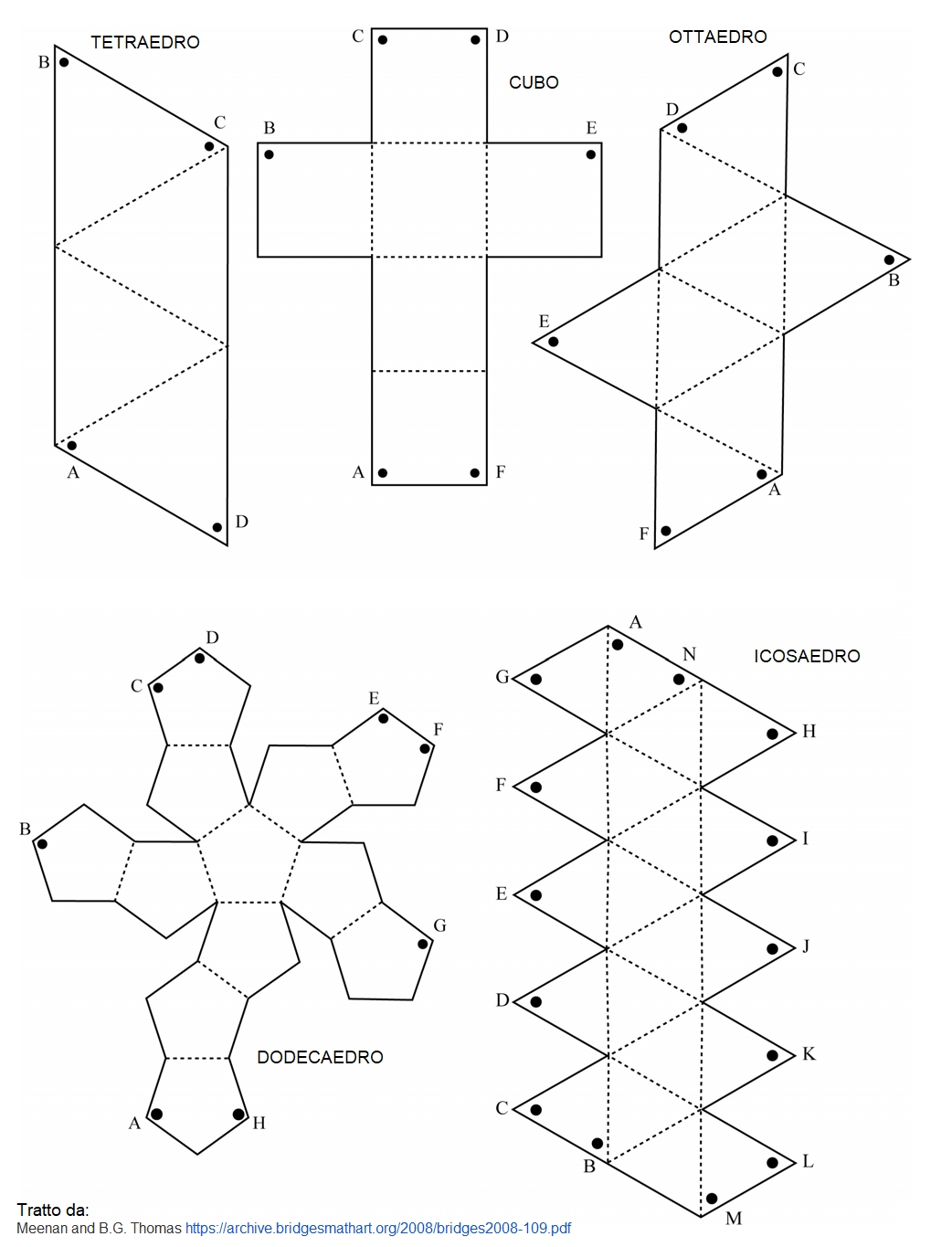
Laboratorio
Alcuni accorgimenti:
- realizza i fori con la punta del compasso
- utilizza fili abbastanza sottili, e aiutati con un ago (con la supervisione di un adulto)
- fai molta attenzione al verso in cui inserire i fili all’interno dei fori
Scarica il file in formato pdf per l’esercitazione del video
Vai agli articoli relativi a:
Sviluppo di un prisma a base esagonale
Sviluppo di un tetraedro
Sviluppo di una piramide a base quadrata
Fonti:
Wikipedia, Youmath, tecnologialanzi.blogspot.com
Potrebbero interessarti anche: