Le proiezioni assonometriche, o più comunemente assonometrie, spiegate con le ombre del Sole. Guarda questo breve e semplice video introduttivo del canale youtube Tecnologia Duepuntozero, oppure leggi l’articolo
Se può esserti utile, scarica lo schema in formato pdf
Un particolare ringraziamento al prof. Raffaele Roma per aver concesso l’utilizzo di porzioni delle riprese da lui realizzate per il video “ASSONOMETRIA E PROSPETTIVA: COSA SONO? (160)” del canale youtube “Romaprof”
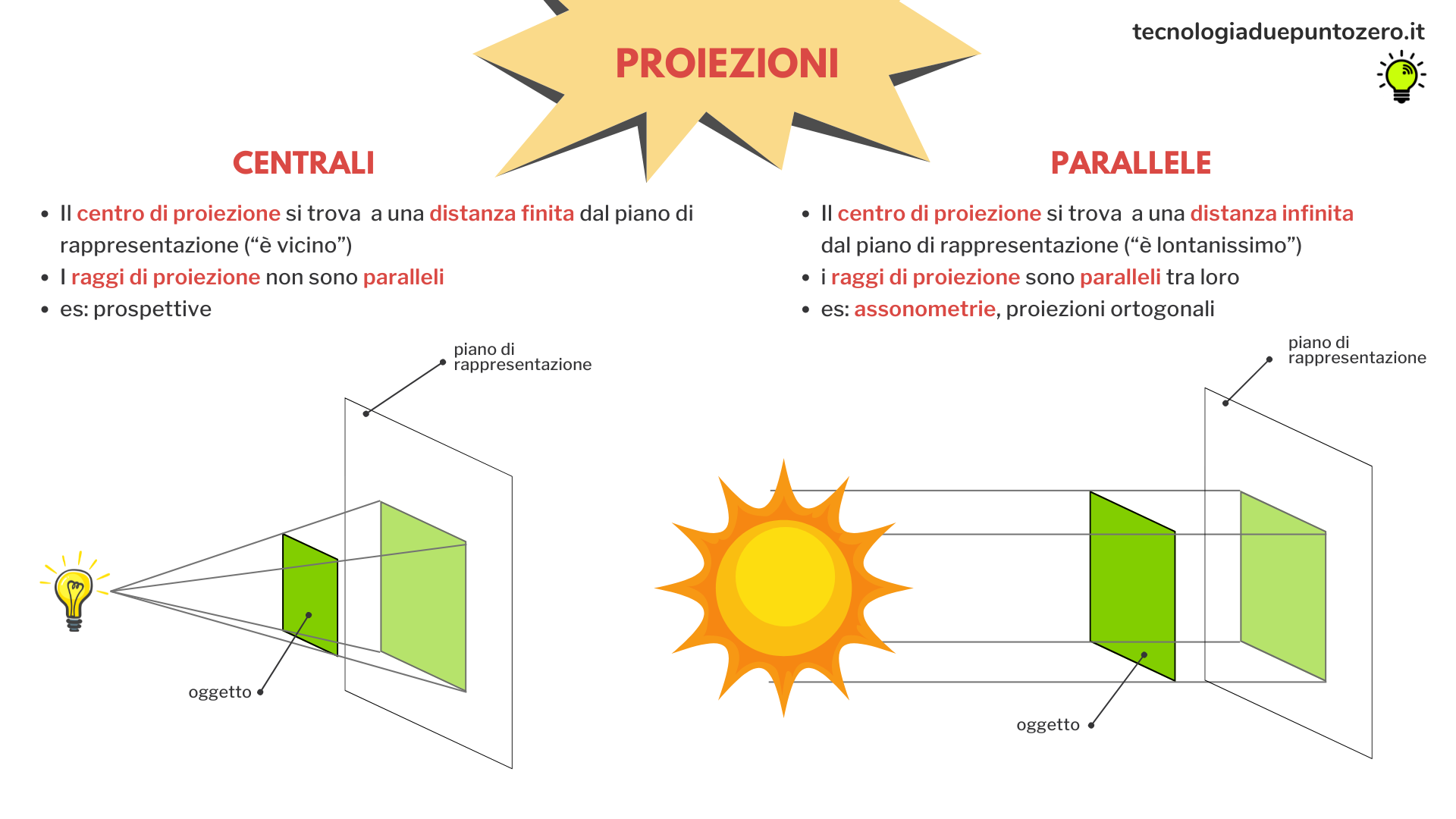
Proiezioni centrali e proiezioni parallele
Le assonometrie
Le proiezioni assonometriche, o più comunemente assonometrie, sono un metodo efficace per rappresentare un oggetto tridimensionale con una sola immagine, fornendo tutte le informazioni relative alle sue dimensioni.
L’effetto che si ottiene è abbastanza simile alla nostra percezione della realtà, ma in certi casi può dar luogo a effetti illusionistici e deformanti.
Le assonometrie fanno parte, insieme alle proiezioni ortogonali, delle proiezioni parallele.
Le assonometrie si ottengono proiettando con raggi paralleli tra loro un oggetto su un piano di proiezione, detto quadro assonometrico, o più semplicemente quadro.
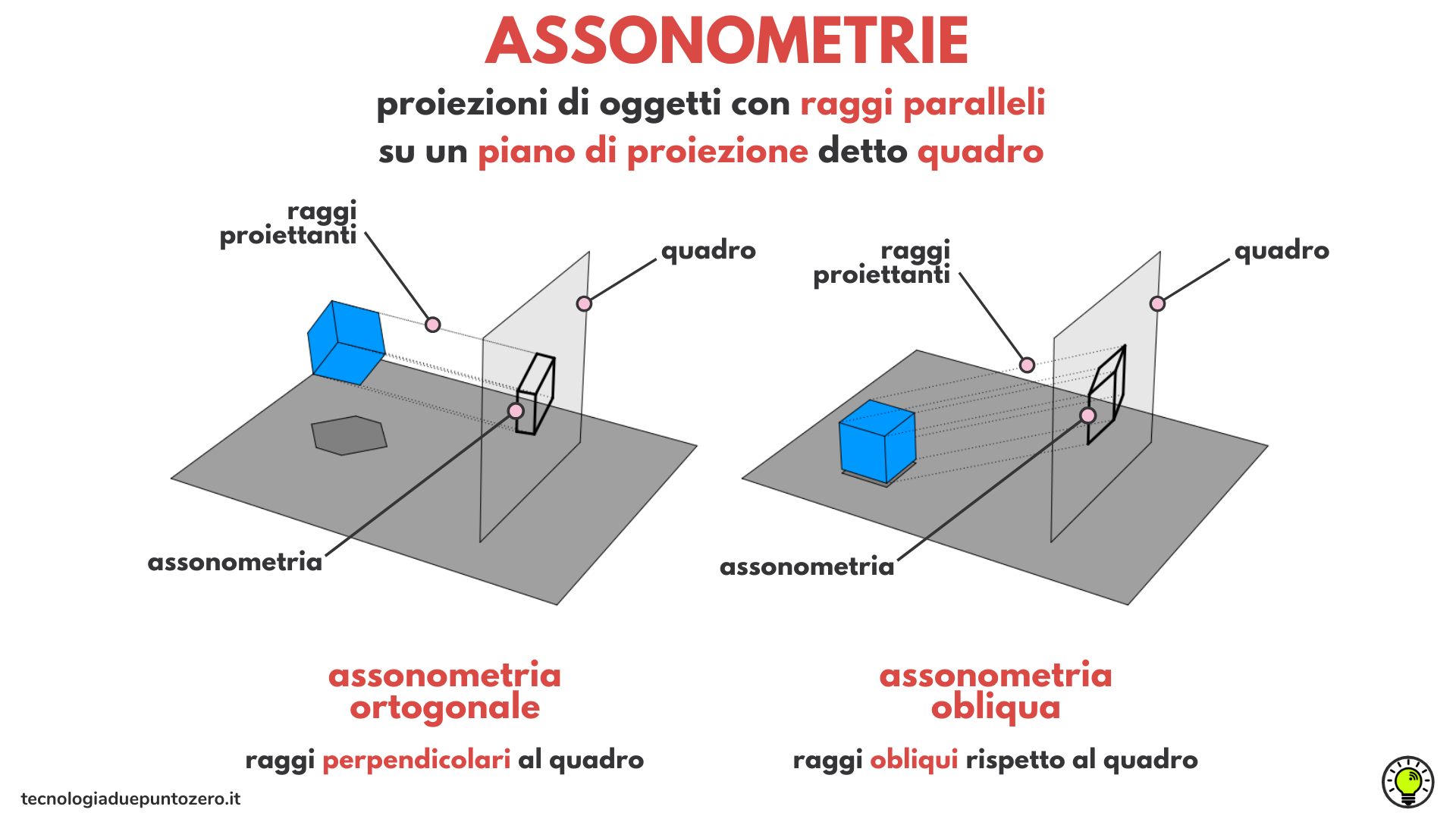
Assonometrie ortogonali e oblique
Quando i raggi proiettanti sono
- perpendicolari al quadro, si parla di assonometria ortogonale
- obliqui rispetto al quadro, si parla di assonometria obliqua
Vista la notevole distanza del Sole dalla Terra, possiamo considerare i raggi del Sole paralleli tra loro, e quindi pensare alle assonometrie come alle ombre di oggetti – geometrici o reali – generate dal Sole su un piano, il quadro.

Conservazione del parallelismo
Guardiamo l’ombra di questo parallelepipedo su questo foglio bianco, prodotta dal Sole. Il foglio è il nostro piano di proiezione, cioè il quadro. Possiamo dire che questa ombra è un’assonometria del parallelepipedo. Cosa possiamo osservare?

Alcuni spigoli di questo parallelepipedo sono paralleli tra loro (a meno di imperfezioni dovuta alla produzione artigianale dell’oggetto). Noto che anche le loro ombre, cioè le proiezioni degli spigoli sul foglio, sono parallele tra loro, comunque io orienti il parallelepipedo.
Posso dire che gli elementi geometrici che nella realtà sono paralleli, si mantengono paralleli anche nella proiezione assonometrica sul quadro (conservazione del parallelismo)
Inoltre, se provo a sovrapporre le ombre di due basi opposte del parallelepipedo (la base più vicina e la base più lontana), vedo che coincidono perfettamente, anche se si trovano a una distanza diversa dal piano di proiezione. La dimensione delle ombre non varia nemmeno al variare della distanza del parallelepipedo dal piano di proiezione.

Assonometria ortogonale
Guardiamo questo sistema di tre assi di riferimento, per esempio asse x, asse y, asse z. I tre assi hanno tutti la stessa lunghezza.

Il piano di proiezione, cioè il foglio bianco, in questo momento è perpendicolare alla direzione dei raggi solari. Il sistema di ombre che ottengo in questo modo è detto assonometria ortogonale.
Mantenendo il quadro ortogonale ai raggi proiettanti, cioè i raggi solari, se si varia l’inclinazione degli assi rispetto al quadro, si ottengono infinite immagini assonometriche.
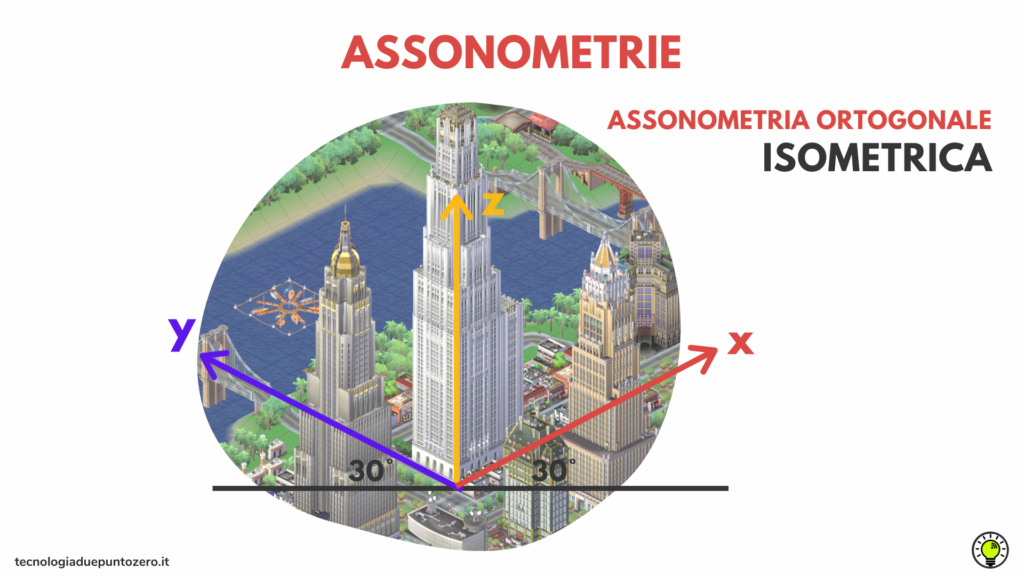
Assonometria isometrica
L’assonometria isometrica è un particolare tipo di assonometria ortogonale, che si ottiene se appoggio le estremità dei tre assi sul foglio.

L’assonometria isometrica è un’assonometria ortogonale in cui il quadro è ugualmente inclinato rispetto ai tre assi.
Osservo che le ombre – cioè le proiezioni – degli assi formano tra loro tre angoli uguali di 120°.
Inoltre, se le misurassi, vedrei che le ombre dei tre assi hanno la stessa lunghezza, che è leggermente inferiore rispetto a quella degli assi reali a causa dell’inclinazione rispetto al piano di proiezione. Questo tipo di assonometria ortogonale viene detta assonometria isometrica, perché le lunghezze delle proiezioni dei tre assi hanno subito la stessa riduzione (iso = uguale).
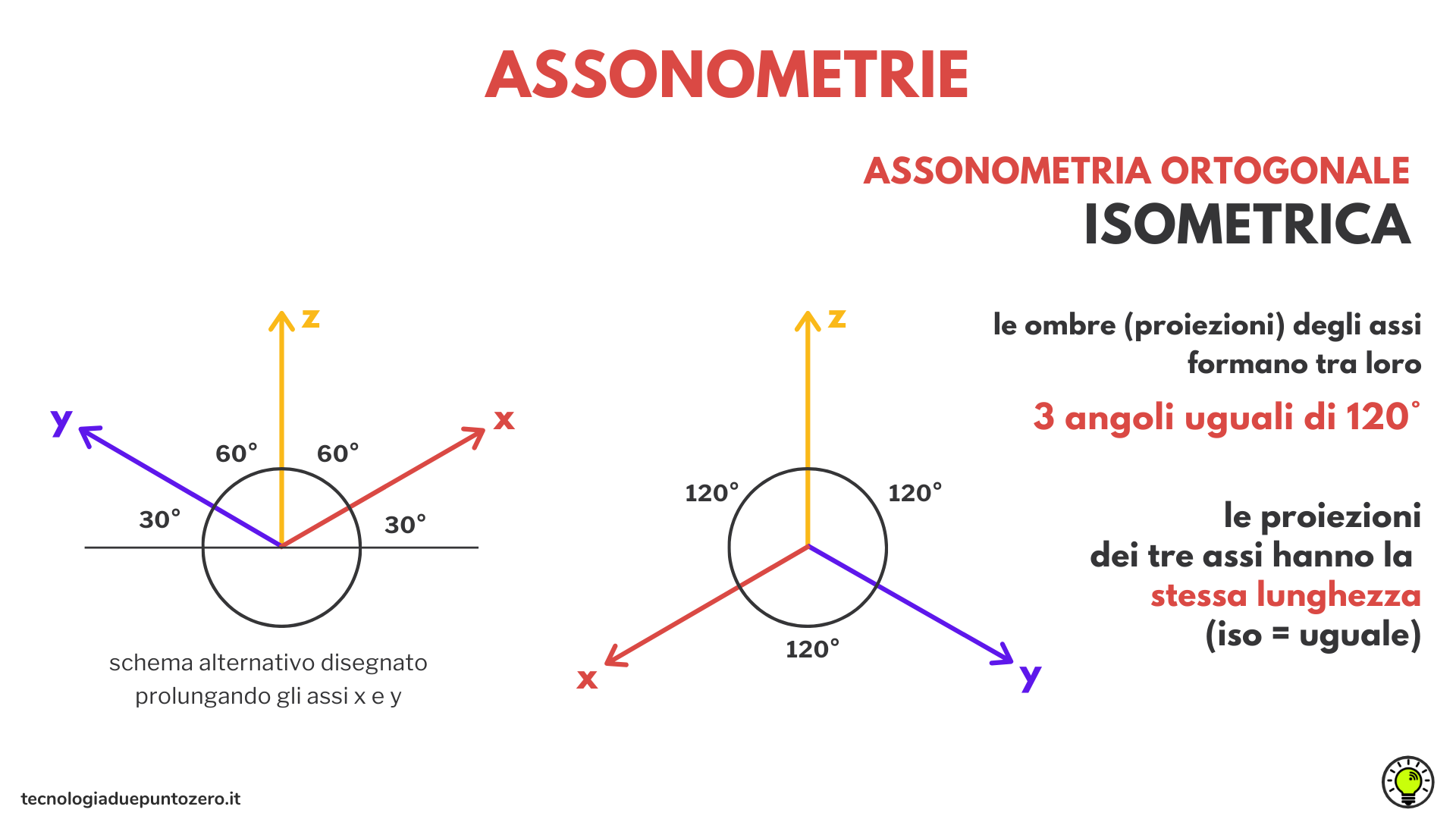
Prolungando gli assi x e y, si può anche disegnare il secondo schema illustrato.
Assonometria obliqua
Se il piano di proiezione, cioè il foglio bianco, non è perpendicolare alla direzione dei raggi solari, si parla di assonometria obliqua.
Assonometria cavaliera
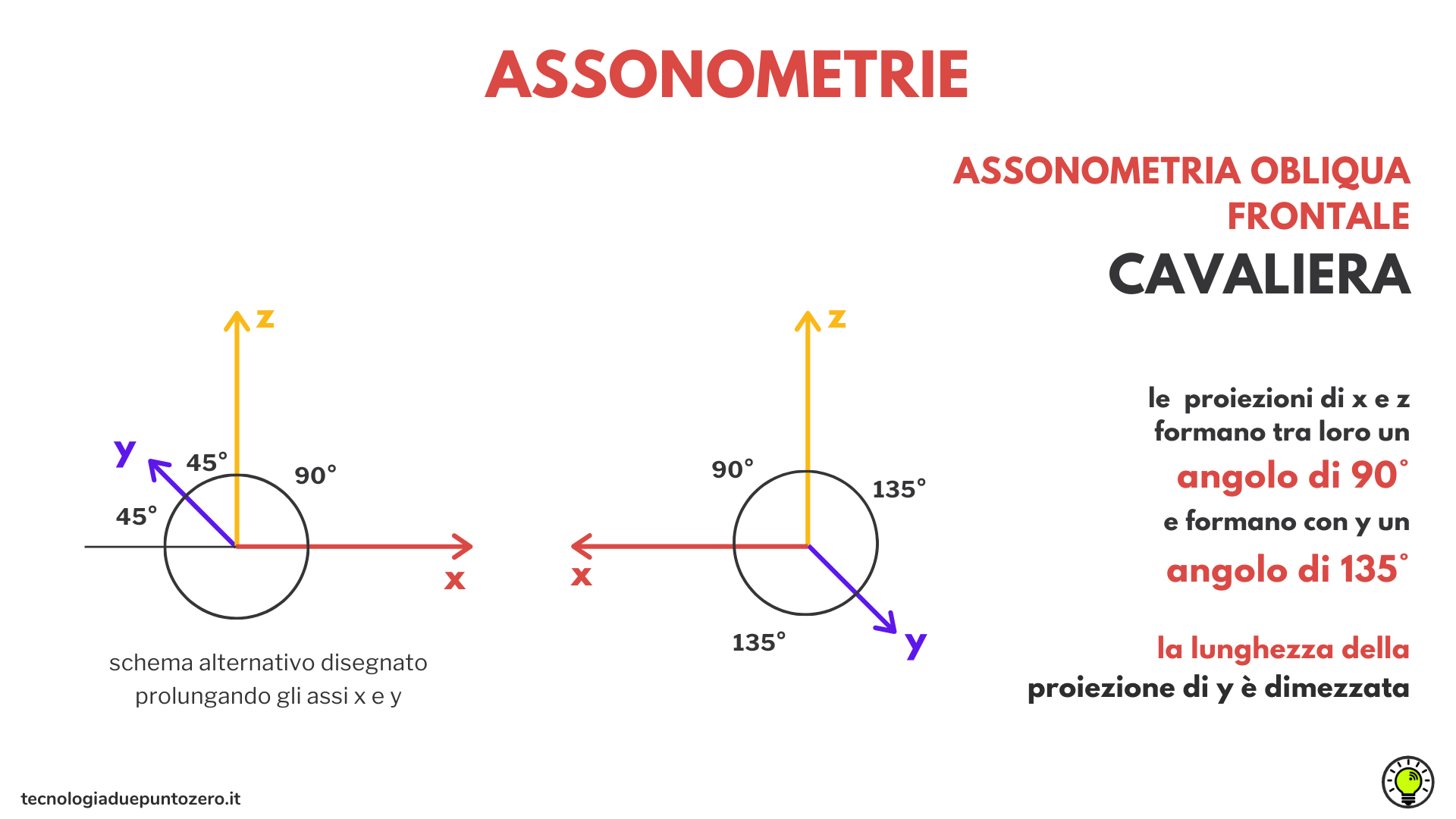
Disponiamo il piano di proiezione (quadro) in posizione verticale. Appoggiamo gli assi x e z del sistema di riferimento sul quadro. L’ asse y fuoriesce dal quadro, e la sua ombra viene proiettata sul piano di proiezione. Delle tre ombre, solo le ombre degli assi x e z, che si trovano sul piano di proiezione, coincidono con gli assi stessi. Questo tipo di assonometria è detto assonometria obliqua frontale. Se mantengo il quadro in posizione verticale, e lo oriento rispetto ai raggi proiettanti in modo che la proiezione dell’asse y abbia una lunghezza pari alla metà dell’asse y reale, ottengo un’assonometria cavaliera.

L’assonometria cavaliera è un’assonometria obliqua in cui gli assi x e z giacciono sul quadro, e i raggi proiettanti sono orientati in modo che la lunghezza della proiezione dell’asse y delle profondità risulti ridotta della metà.
I tre assi x, y, z proiettati sul quadro individuano un angolo di 90° e due di 135°. Prolungando gli assi x e y, si ottiene anche lo schema usuale di 90° – 45° – 45°.
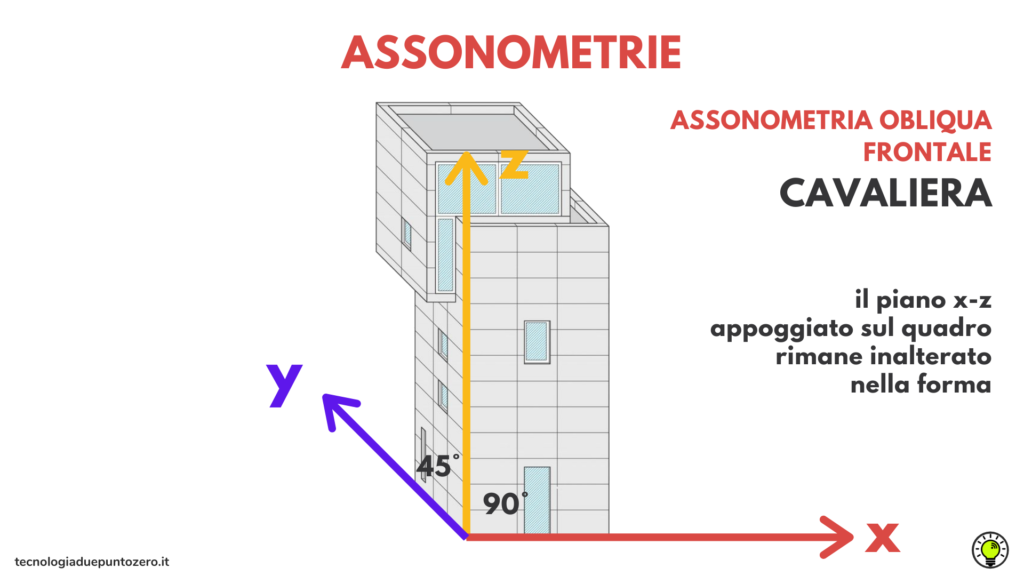
Che caratteristica ha l’assonometria cavaliera rispetto a quella isometrica? Che il piano x-z appoggiato sul quadro rimane inalterato nella forma, e con lui, tutti i piani ad esso paralleli. Infatti, gli angoli tra le ombre degli assi sono uguali a quelli tra gli assi reali.

Se appoggio una faccia di questo parallelepipedo sul piano di proiezione, cioè sul quadro, anche l’ombra della faccia opposta, cioè quella più vicina alla videocamera resta di forma inalterata: è un rettangolo. Questo accade anche se si stacca il parallelepipedo dal quadro, mantenendolo parallelo a sé stesso. Le due facce parallele al quadro, quella più vicina e quella più lontana dalla telecamera, non si deformano, ma restano rettangolari. Se immagino che questo parallelepipedo sia un edificio, la sua facciata resta inalterata nelle misure e nella forma. In questa assonometria la faccia frontale non si deforma: l’effetto è quello di una vista frontale.
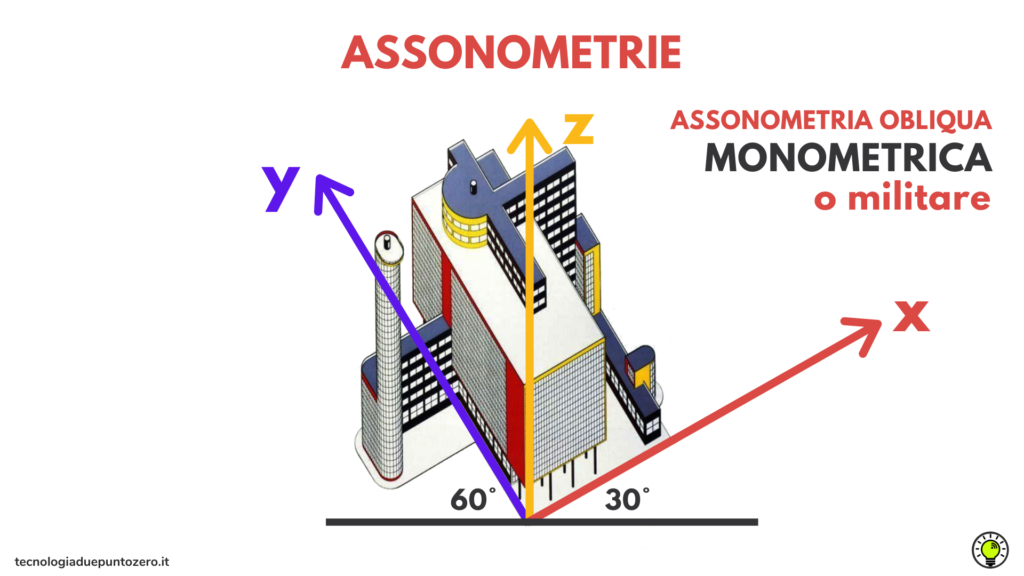
Assonometria monometrica o militare
Disponiamo il piano di proiezione (quadro) in posizione orizzontale. Appoggio la base del parallelepipedo sul quadro: le misure e la forma della proiezione della base rispetto alla base reale non cambiano. Se immagino che questo parallelepipedo sia un edificio, con questa assonometria la sua pianta resta inalterata nelle misure e nella forma.

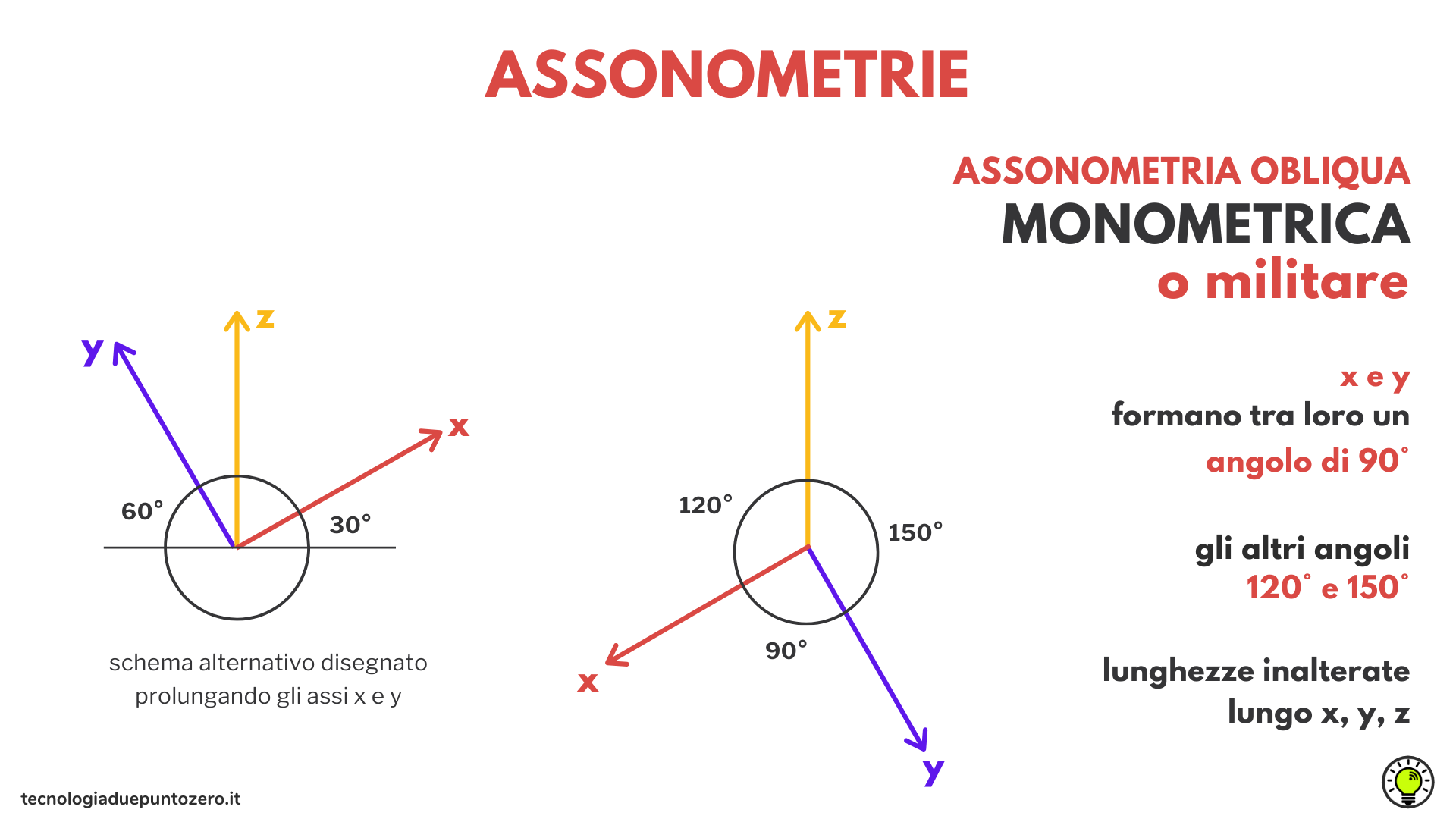
In pratica si appoggiano gli assi x e y del sistema di riferimento sul quadro. L’ asse z fuoriesce dal quadro, e la sua ombra viene proiettata sul piano di proiezione. Se oriento il quadro rispetto ai raggi proiettanti in modo che la lunghezza della proiezione dell’asse z risulti uguale a quella dell’asse z reale, ottengo un’assonometria monometrica. Quindi nell’assonometria monometrica le misure non subiscono variazioni su nessuno degli assi x, y, z.
L’assonometria monometrica è un’assonometria obliqua in cui gli assi x e y giacciono sul quadro, e i raggi proiettanti sono orientati in modo che la lunghezza della proiezione dell’asse z delle altezze risulti invariata.
L’assonometria monometrica è chiamata anche militare perché le immagini ottenute assomigliano a viste aeree: per questo motivo è stata largamente usata in ambito militare.
Nell’assonometria monometrica, gli assi x e y formano tra loro un angolo di 90°, mentre gli altri angoli sono di 120° e 150°. Prolungando gli assi x e y, si ottiene anche lo schema usuale di 90° – 30° – 60°.
Tratto da:
Video “ASSONOMETRIA E PROSPETTIVA: COSA SONO? (160)” del canale youtube “Romaprof” (su gentile concessione del prof. Raffaele Roma)
Tecnologia, progettazione, ambiente – S. Rosano – Zanichelli
Progettare e fare – G. Paci, R. Paci – Zanichelli
Disegnare nel progetto – E. Bartolucci – REDA edizioni per l’agricoltura
Potrebbero interessarti anche:

